Приведенные ниже уроки разработаны в виде лекций, так как эта форма, по моему мнению, является наиболее производительной и оставляет в данном случае достаточно времени для работы с динамическими демонстрационными моделями. При желании эта форма  может быть легко трансформирована в любую другую форму проведения урока.

УРОК № 1.

Тема урока: Колебательный контур. Превращения энергии в колебательном контуре.

Объяснение нового материала.

Цель урока: объяснение понятия колебательного контура и сути электромагнитных колебаний с использованием динамической модели “Идеальный колебательный контур”.

Колебания могут происходить в системе, которая называется колебательным контуром, состоящим из конденсатора емкостью С и катушки индуктивностью L. Колебательный контур называется идеальным, если в нем нет потерь энергии на нагревание соединительных проводов и проводов катушки, т. е. пренебрегают сопротивлением R.

(Именно такой идеальный колебательный контур вы видите на экранах. Это - динамическая модель колебательного процесса, которая поможет нам разобраться с основными понятиями и законами электромагнитных колебательных процессов. Здесь вы видите источник тока схематичные изображения конденсатора  и катушки индуктивности).

Давайте сделаем в тетрадях чертеж схематичного изображения колебательного контура.

Чтобы возникли электрические колебания в этом контуре, ему необходимо сообщить некоторый запас энергии, т.е. зарядить конденсатор. Когда конденсатор зарядится, то электрическое поле будет сосредоточено между его пластинами.

(Давайте проследим процесс зарядки конденсатора и остановим процесс, когда зарядка будет завершена).

 

 

 

Итак, конденсатор заряжен, его энергия равна

, но ,

поэтому  , следовательно,

.

Так как после зарядки конденсатор будет иметь максимальный заряд (обратите внимание на пластины конденсатора, на них расположены противоположные по знаку заряды), то при q=qmax  энергия электрического поля конденсатора будет максимальна и равна

.

В начальный момент времени вся энергия сосредоточена между пластинами конденсатора, сила тока в цепи равна нулю. (Давайте теперь замкнем на нашей модели конденсатор на катушку). При замыкании конденсатора на катушку он начинает разряжаться и в цепи возникнет ток, который, в свою очередь, создаст в катушке магнитное поле. Силовые линии этого магнитного поля направлены по правилу буравчика.

          При разрядке конденсатора ток не сразу достигает своего максимального значения, а постепенно. Это происходит потому, что переменное магнитное поле порождает в катушке второе электрическое поле. Вследствие явления самоиндукции там возникает индукционный ток, который, согласно правилу Ленца, направлен в сторону, противоположную увеличению разрядного тока.

           Когда разрядный ток достигает своего максимального значения энергия магнитного поля максимальна и равна

,

а энергия конденсатора в этот момент равна нулю. Таким образом, через t=T/4 энергия электрического поля полностью перешла в энергию магнитного поля.

(Давайте понаблюдаем процесс разрядки конденсатора на динамической модели. Обращаю ваше внимание на то, что такой способ представления процессов зарядки и разрядки конденсатора в виде потока перебегающих частиц, является условным и выбран для удобства восприятия. Вы прекрасно знаете, что скорость движения электронов очень мала (порядка нескольких сантиметров в секунду). Итак, вы видите, как, при уменьшении заряда на конденсаторе изменяется сила тока в цепи, как изменяются энергии магнитного и электрического полей, какая между этими изменениями существует связь.  Так как контур является идеальным, то потерь энергии нет, поэтому общая энергия контура остается постоянной).

          С началом перезарядки конденсатора разрядный ток будет уменьшаться до нуля не сразу, а постепенно. Это происходит опять же из-за возникновения противо э. д. с. и индукционного тока противоположной направленности. Этот ток противодействует уменьшению разрядного тока, как ранее противодействовал его увеличению. Сейчас он будет поддерживать основной ток. Энергия магнитного поля будет уменьшаться, энергия электрического – увеличиваться, конденсатор будет перезаряжаться.

          Таким образом, полная энергия колебательного контура в любой момент времени равна сумме энергий магнитного и электрического полей

          Колебания, при которых происходит периодическое превращение энергии электрического поля конденсатора в энергию магнитного поля катушки, называются ЭЛЕКТРОМАГНИТНЫМИ колебаниями. Так как эти колебания происходят за счет первоначального запаса энергии и без внешних воздействий, то они являются СВОБОДНЫМИ.

Урок 2

.

Тема урока: Аналогия между механическими и электромагнитными колебаниями

.

Объяснение нового материала.

Цель урока: объяснение сути и доказательство аналогии между электромагнитными колебаниями и колебаниями пружинного маятника с использованием динамической колебательной модели ”Аналогия между механическими и электромагнитными колебаниями” и презентаций PowerPoint.

Материал для повторения:

·        понятие колебательного контура;

·        понятие идеального колебательного контура;

·        условия возникновения колебаний в к/к;

·        понятия магнитного и электрического полей;

·        колебания как процесс периодического изменения энергий;

·        энергия контура в произвольный момент времени;

·        понятие (свободных) электромагнитных колебаний.

(Для повторения и закрепления учащимся еще раз демонстрируется динамическая модель идеального колебательного контура).

На этом уроке мы рассмотрим аналогию между механическими и электромагнитными колебаниями. В качестве механической колебательной системы будем рассматривать пружинный маятник. 

(На экране вы видите динамическую модель, которая демонстрирует аналогию между механическими и электромагнитными колебаниями. Она поможет нам разобраться в колебательных процессах, как в механической системе, так и в электромагнитной).

Итак, в пружинном маятнике упругодеформированная пружина сообщает скорость  прикрепленному к ней грузу. Деформированная пружина обладает потенциальной энергией упругодеформированного тела

,

движущийся груз обладает кинетической энергией

.

Превращение потенциальной энергии пружины в кинетическую энергию колеблющегося тела является механической аналогией превращения энергии электрического поля конденсатора в энергию магнитного поля катушки. При этом аналогом механической потенциальной энергии пружины  является энергия электрического поля конденсатора, а аналогом механической кинетической энергии груза является энергия магнитного поля, которая связана с движением зарядов. Зарядке конденсатора от батареи соответствует сообщение  пружине потенциальной энергии (например, смещение рукой).

 Давайте сопоставим формулы и выведем общие закономерности для электромагнитных и механических колебаний.

                ПРУЖИНА                                                                КОНДЕНСАТОР

                                                                 

                        ГРУЗ                                       КАТУШКА

                                                           

Из сопоставления формул следует, что аналогом индуктивности L является масса m,  а аналогом смещения х служит заряд q, аналогом коэффициента k служит величина, обратная электроемкости, т. е. 1/С.

Моменту, кода конденсатор разрядится, а сила тока достигнет максимума, соответствует прохождение телом положения равновесия с максимальной скоростью (обратите внимание на экраны: там вы можете пронаблюдать это соответствие).

          Далее при перезарядке конденсатора тело будет смещаться влево от положения равновесия. Через промежуток времени, равный t=T/2, конденсатор полностью перезарядится и сила тока в цепи станет равной нулю.

          Как уже было сказано на прошлом занятии, движение электронов по проводнику является условным, ведь для них основным видом движения является колебательное движение около положения равновесия. Поэтому иногда еще электромагнитные колебания сравнивают с колебаниями воды в сообщающихся сосудах (посмотрите на экран, вы видите, что в правом верхнем углу находится именно такая колебательная система), где каждая частица совершает колебания около положения равновесия.

          Итак, мы выяснили, что аналогией индуктивности является масса, а аналогией перемещения является заряд. Но вед вы прекрасно знаете, что изменение заряда в единицу времени – это не что иное, как сила тока, а изменение координаты в единицу времени – скорость, то есть q’

= I, а  x’

= v. Таким образом, мы нашли еще одно соответствие между механическими и электрическими величинами.

          Давайте составим таблицу, которая поможет нам систематизировать связи механических и электрических величин при колебательных процессах.

 

 

Таблица соответствия между механическими и электрическими величинами при колебательных процессах.

Механические величины	Электрические величины
Координата х	Заряд q
Скорость vx	Сила тока i
Масса m	Индуктивность L
Потенциальная энергия kx2/2	Энергия электрического поля q2/2
Жесткость пружины k	Величина, обратная емкости 1/C
Кинетическая энергия mv2/2	Энергия магнитного поля Li2/2

 

 

 

Урок 2.

Тема урока: Уравнение свободных гармонических колебаний в контуре. Колебаний.

Объяснение нового материала.

Цель урока: вывод основного уравнения электромагнитных колебаний, законов изменения заряда и силы тока, получения формулы Томсона и выражения для собственной частоты колебания контура с использованием презентаций PowerPoint.

Материал для повторения:

·        понятие электромагнитных колебаний;

·        понятие энергии колебательного контура;

·        соответствие электрических величин механическим величинам при колебательных процессах.

(Для повторения и закрепления необходимо еще раз продемонстрировать модель аналогии механических и электромагнитных колебаний).

          На прошлых уроках мы выяснили, что электромагнитные колебания, во-первых, являются свободными, во-вторых, представляют собой периодическое изменение энергий магнитного и электрического полей. Но кроме энергии при электромагнитных колебаниях меняется еще и заряд, а значит и сила тока в контуре и напряжение. На этом уроке мы должны выяснить законы, по которым меняются заряд, а значит сила тока и напряжение.

  Итак, мы выяснили, что полная энергия колебательного контура в любой момент времени равна сумме энергий магнитного и электрического полей:  . Считаем, энергия не меняется со временем, то есть контур – идеальный. Значит производная полной энергии по времени равна нулю, следовательно, равна нулю сумма производных по времени от энергий магнитного и электрического полей:

, то есть .

          Знак минус в этом выражении означает, что когда энергия магнитного поля возрастает, энергия электрического поля убывает и наоборот. А физический смысл этого выражения таков, что скорость изменения энергии магнитного поля равна по модулю и противоположна по направлению скорости изменения электрического поля.

          Вычисляя производные, получим

.

          Но   ,   поэтому    и 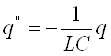 - мы получили уравнение, описывающее свободные электромагнитные колебания в контуре. Если теперь мы заменим q на x,  х’’=ах на q’’, k на 1/C, m на L, то  получим уравнение 

,

описывающее колебания груза на пружине. Таким образом, уравнение электромагнитных колебаний имеет такую же математическую форму, как уравнение колебаний пружинного маятника.

          Как вы видели на демонстрационной модели, заряд на конденсаторе меняется периодически. Необходимо найти зависимость заряда от времени.

          Из девятого класса вам знакомы периодические функции синус и косинус. Эти функции обладают следующим свойством: вторая производная синуса и косинуса пропорциональна самим функциям, взятым с противоположным знаком. Кроме этих двух, никакие другие функции этим свойством не обладают. А теперь вернемся к электрическому заряду. Можно смело утверждать, что электрический заряд, а значит и сила тока, при свободных колебаниях меняются с течением времени по закону косинуса или синуса, т. е. совершают гармонические колебания. Пружинный маятник также совершают гармонические колебания (ускорение пропорционально смещению, взятому со знаком минус).

          Итак, чтобы найти явную зависимость заряда, силы тока и напряжения от времени, необходимо решить уравнение

,

учитывая гармонический характер изменения этих величин.

          Если в качестве решения взять выражение типа q = qm cos t , то, при подстановке этого решения в исходное уравнениe, получим q’’=-qmcos t=-q.

Поэтому, в качестве решения необходимо взять выражение вида

q=qmcosωot,

где qm – амплитуда колебаний заряда (модуль наибольшего значения колеблющейся величины),

ωo = - циклическая или круговая частота. Ее физический смысл –

число колебаний за один период, т. е. за 2π с.

          Период электромагнитных колебаний – промежуток времени, в течение которого ток в колебательном контуре и напряжение на пластинах конденсатора совершает одно полное колебание. Для гармонических колебаний Т=2π с (наименьший период косинуса).

          Частота колебаний – число колебаний в единицу времени – определяется так: ν =  .

 Частоту свободных колебаний называют собственной частотой колебательной системы.

 (Посмотрите на экран, перед вами графики зависимости заряда от времени и смещения от времени, представляющие собой косинусоиды).

 

 

 

Так как ωo= 2π ν=2π/Т, то Т= .

Циклическую частоту мы определили как ωo = , значит для периода можно записать

Т=

 = 

- формула Томсона для периода электромагнитных колебаний.

Тогда выражение для собственной частоты колебаний примет вид

.

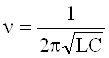Нам осталось получить уравнения колебаний силы тока в цепи  и напряжения на конденсаторе.

          Так как , то при q = qm cos ωo t получим U=Umcosωot. Значит, напряжение тоже меняется по гармоническому закону. Найдем теперь закон, по которому меняется сила тока в цепи.

По определению ,

но q=qmcosωt, поэтому

,

где π/2 – сдвиг фаз между силой тока и зарядом (напряжением). Итак, мы выяснили, что сила тока при электромагнитных колебаниях тоже меняется по гармоническому закону.

 (Посмотрим на экраны, там вы видите графики зависимости заряда и напряжения на конденсаторе и силы тока в цепи от времени. На графиках хорошо видно, что сила тока сдвинута относительно заряда на π/2).

Мы рассматривали идеальный колебательный контур, в котором нет потерь энергии и свободные колебания могут продолжаться бесконечно долго за счет энергии, однажды полученной от внешнего источника. В реальном контуре часть энергии идет на нагревание соединительных проводов и нагревание катушки. Поэтому свободные колебания в колебательном контуре являются затухающими.